Je vous propose cet octaèdre avec changement de couleur de John Szinger crée en 2010


que j'ai decouvert ici


Cette page devrait donner les réponses a tes questionstudor a écrit : Est-ce que tu confirmes que la partie "extérieure" n'est pas une simple grille 7x7, mais un truc un peu plus subtil?
Et donc une seule feuille suffit pour faire l'octaèdre ?
Toi, tu sais parler aux plieurs!rouchka a écrit : Les carrés sont de 2/13
et le modèle est un "single sheet" , donc une seule feuille... c'est pas tentant ça...!?
cecile a écrit :Toi, tu sais parler aux plieurs!




Là, je n'ai pas vraiment compris. Une référence exacte qui devient une approximation jugée satisfaisante... il y a peut-être une faute de frappe?rouchka a écrit : il est a noter que c'est une référence exacte pour obtenir des carrés de 2/13 néanmoins c'est une approximation que l'auteur juge satisfaisante
En fait l'auteur visait l'angle 67,5 et des carrés de 2/13 ont fait une bonne approximation de cet angletudor a écrit :Là, je n'ai pas vraiment compris. Une référence exacte qui devient une approximation jugée satisfaisante... il y a peut-être une faute de frappe?rouchka a écrit : il est a noter que c'est une référence exacte pour obtenir des carrés de 2/13 néanmoins c'est une approximation que l'auteur juge satisfaisante
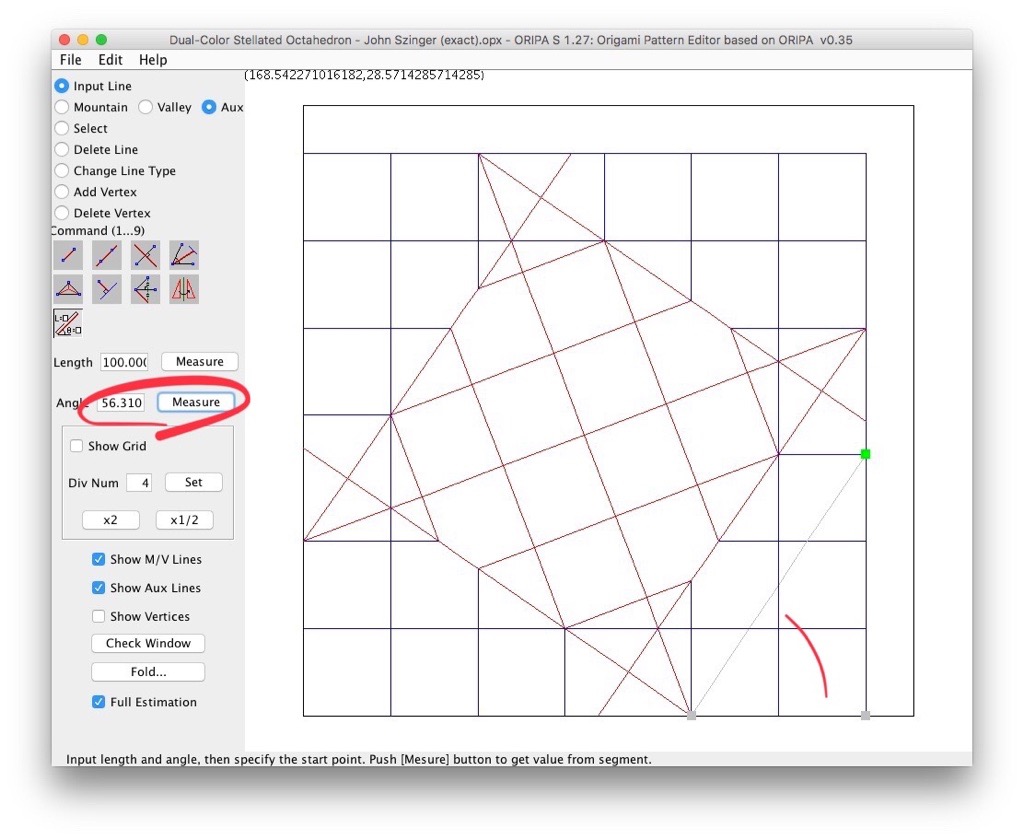
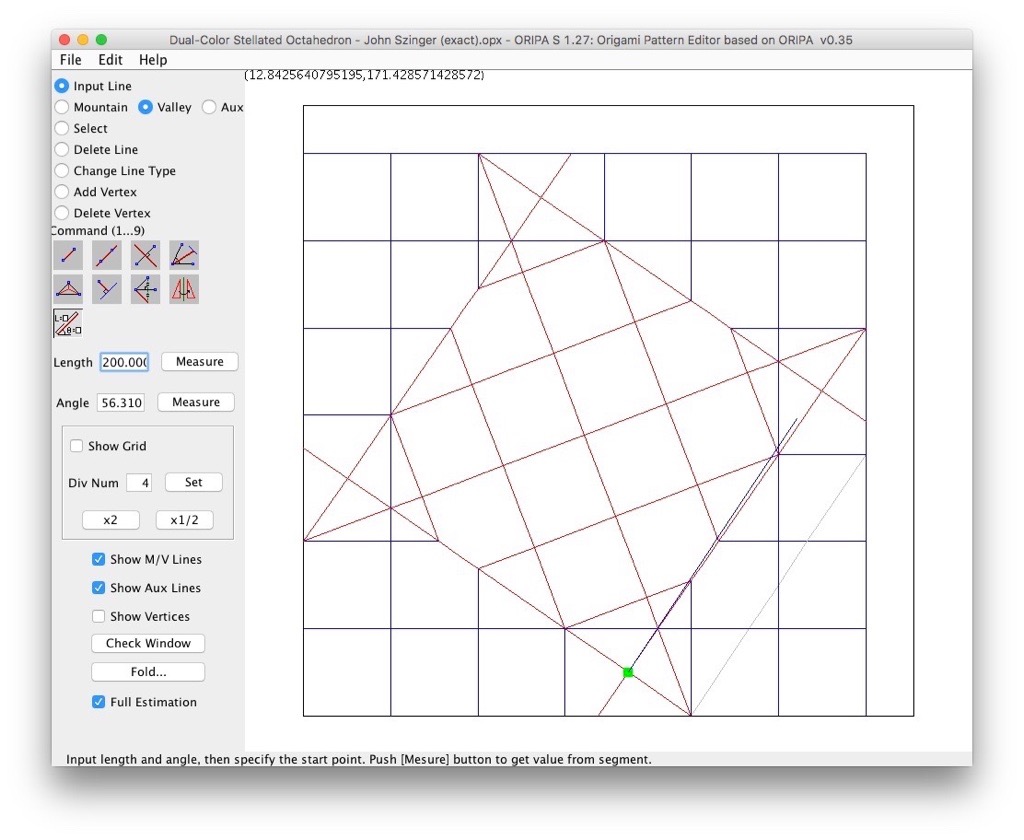
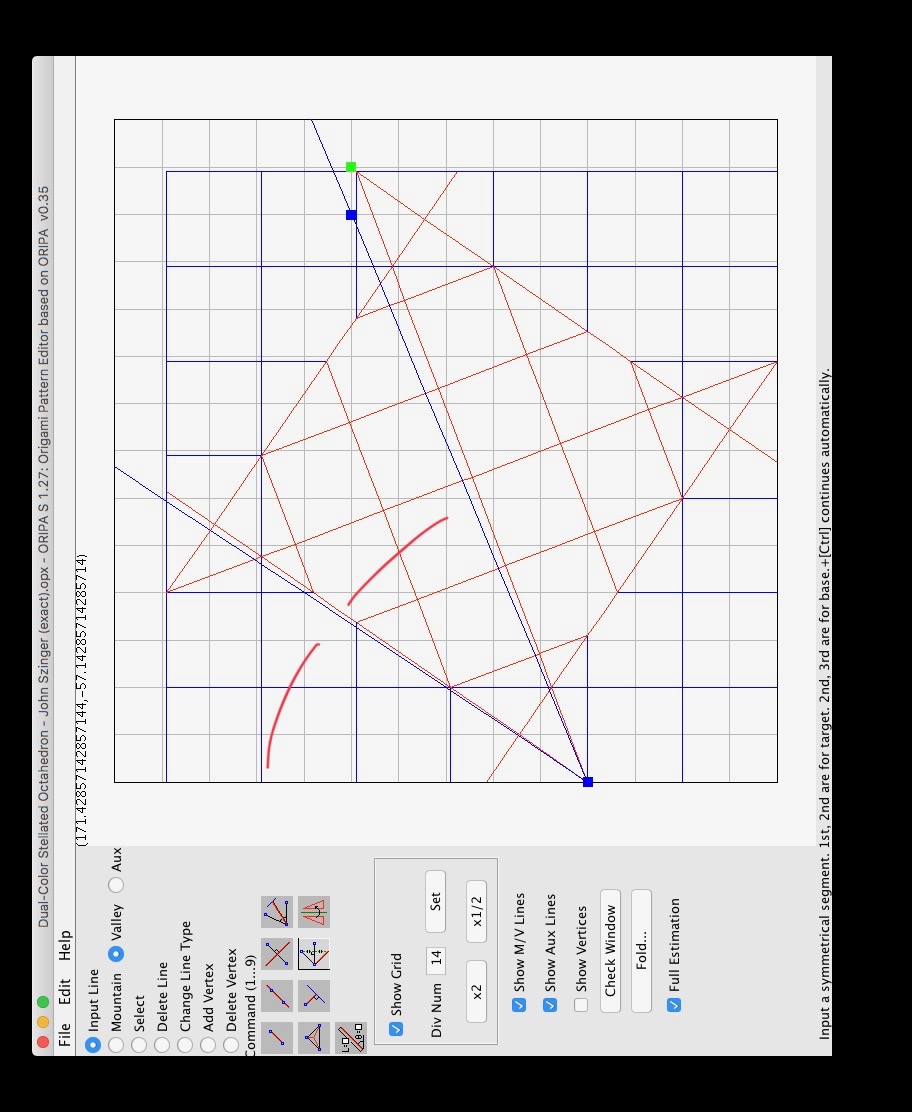
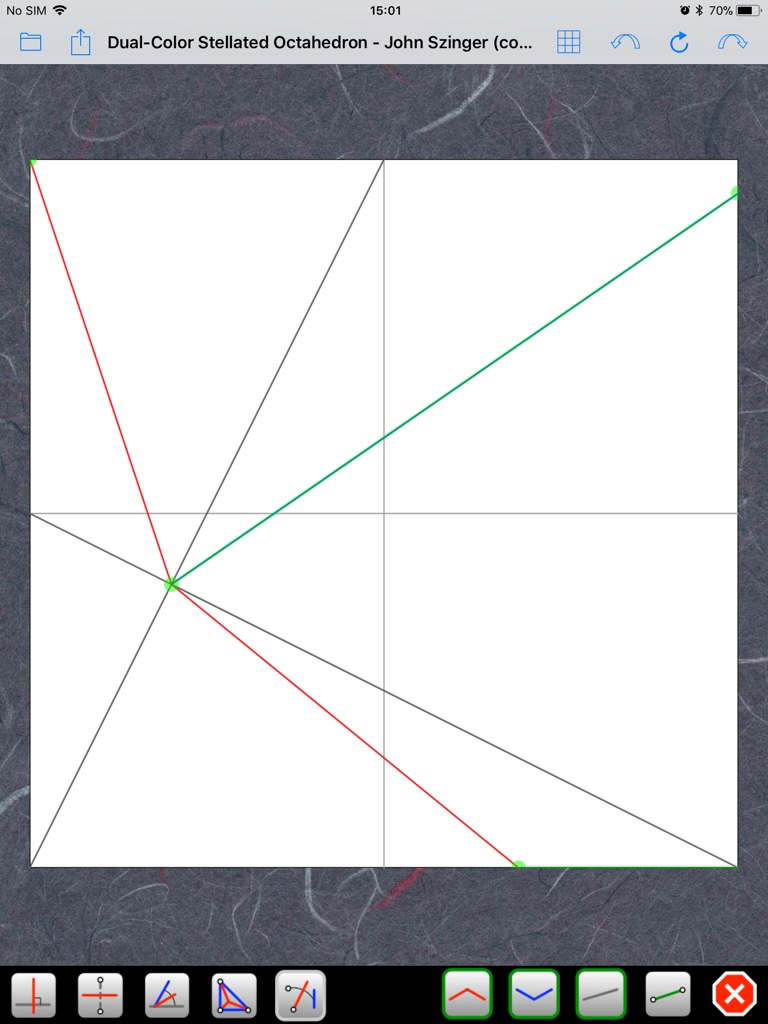
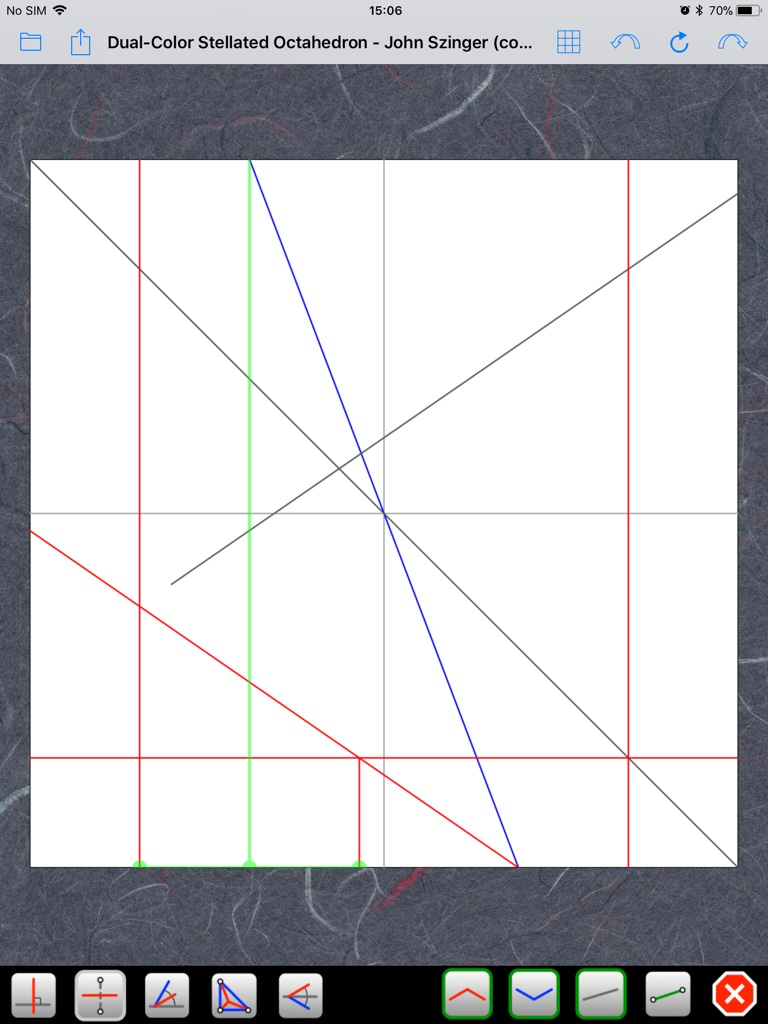
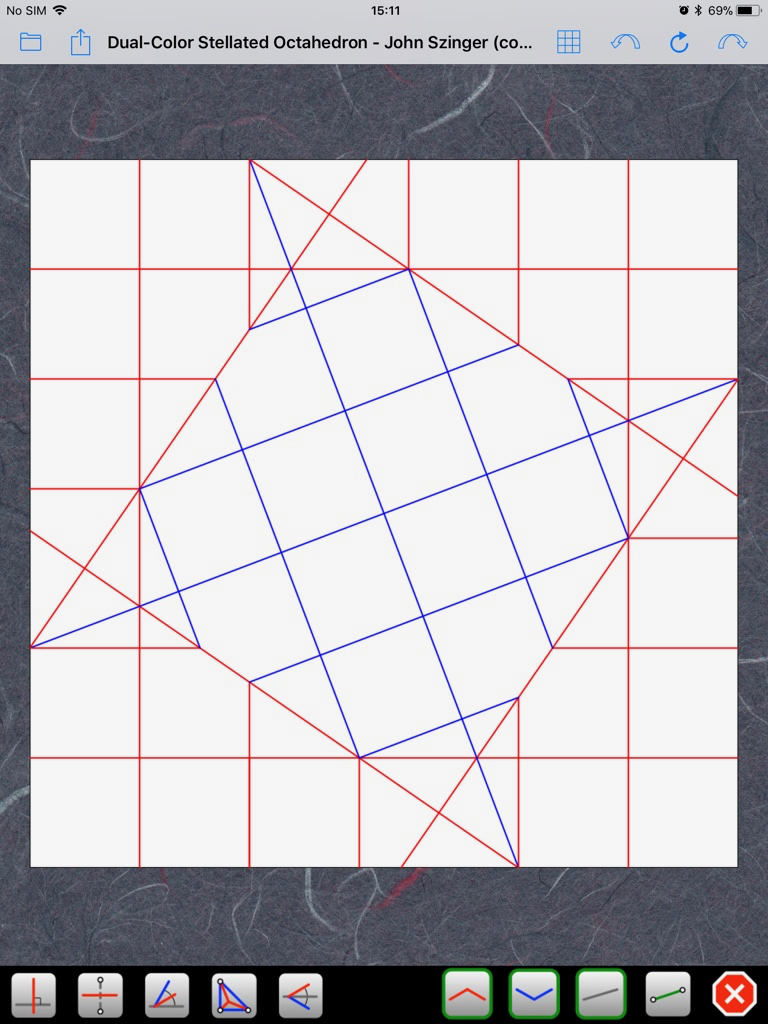
Voici une petite explication supplémentaire. Si on construit le CP de manière exacte, on obtient ceci (cliquez sur les images pour les agrandir):tudor a écrit :Là, je n'ai pas vraiment compris. Une référence exacte qui devient une approximation jugée satisfaisante... il y a peut-être une faute de frappe?rouchka a écrit : il est a noter que c'est une référence exacte pour obtenir des carrés de 2/13 néanmoins c'est une approximation que l'auteur juge satisfaisante
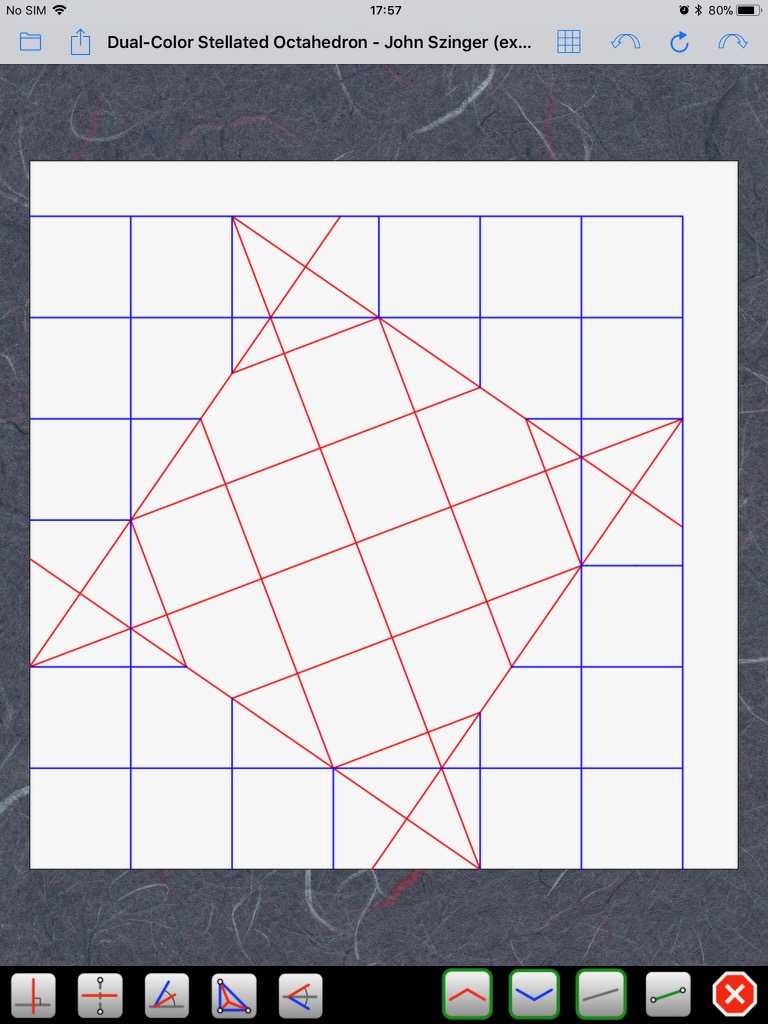
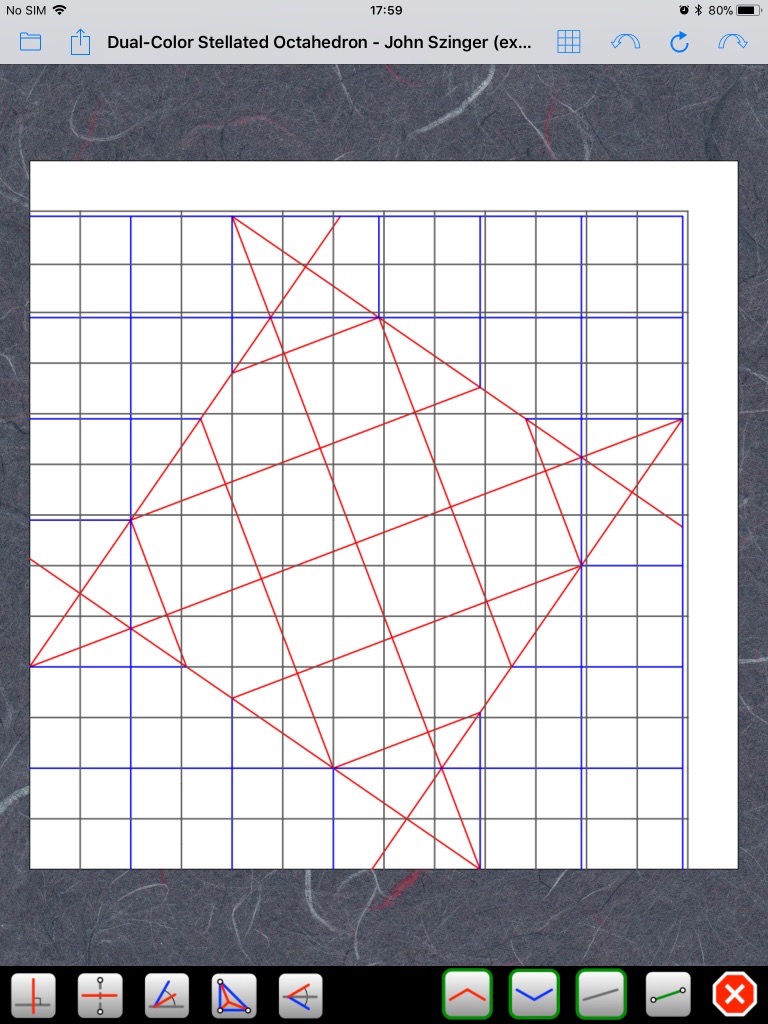
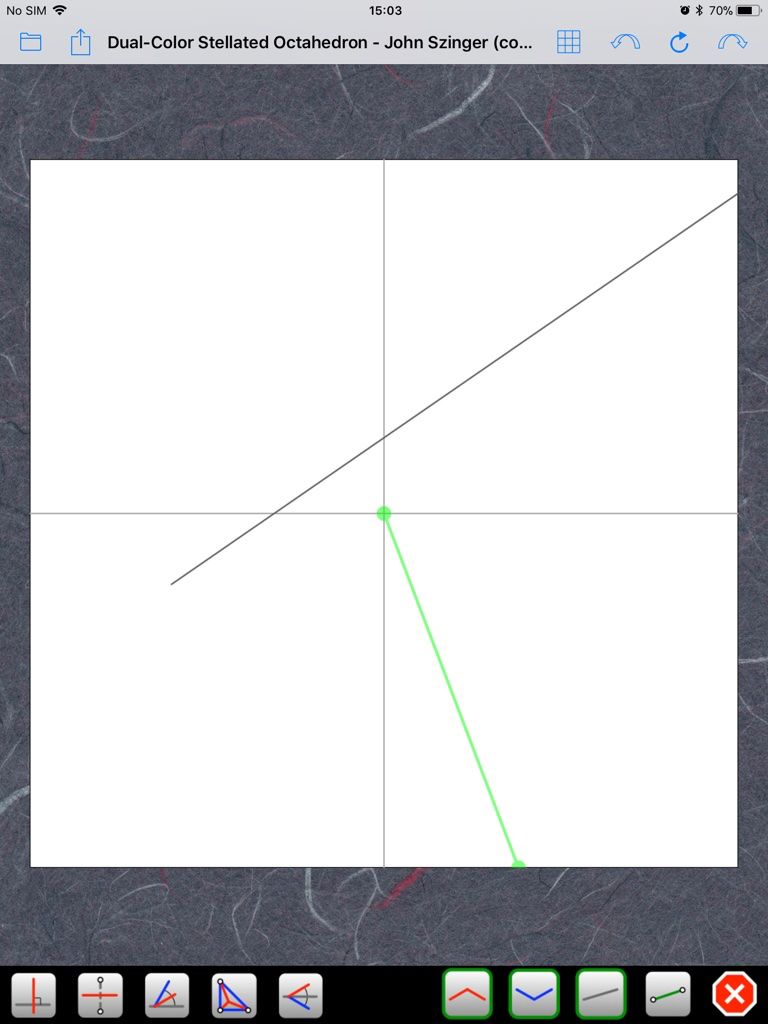
Erreur, cher confrère! Un angle de 67,5 degrés (3/4 d'un angle droit) serait trop facile! Ce CP exact est beaucoup plus difficile à obtenir. Ci-dessus, j'ai triché en commençant par les trois carrés en bas à gauche. Je regarde la diagonale du rectangle formé par les deux derniers carrés et je cherche le pli qui me permet de la rabattre sur la diagonale du papier:rouchka a écrit :En fait l'auteur visait l'angle 67,5 et des carrés de 2/13 ont fait une bonne approximation de cet angle

Nous sommes quittes, moi je n'ai rien essayé sur informatiqueNaoki a écrit :je n'ai encore rien essayé sur papier! Akira
c'est exactement ce que je disait Akira, il aurait voulu avoir cet angle facile a construire mais les contraintes carré de départ & maximum de papier & construction simple (donc valeurs entieres) le poussent vers cette approximation , donc on est bien d'accord ( enfin c'est ce que je crois comprendre)Naoki a écrit :Il n'y a donc pas moyen de construire ce pliage exactement à partir d'une grille. Mais une grille de 13x13 est une bonne approximation.rouchka a écrit : il est a noter que c'est une référence exacte pour obtenir des carrés de 2/13 néanmoins c'est une approximation que l'auteur juge satisfaisante
Erreur, cher confrère! Un angle de 67,5 degrés (3/4 d'un angle droit) serait trop facile! Akirarouchka a écrit :En fait l'auteur visait l'angle 67,5 et des carrés de 2/13 ont fait une bonne approximation de cet angle
il ne te reste plus qu'a plier vallée les carrées et montagne leurs diagonales et finir par un lock et le tour est joué et franchement je ne voit pas vraiment de défaut a ce choix .D'ailleurs le fait que le modèle soit inversible me semble être une contrainte inutile (entre autres) et c'est pour ça que je l'ai omise dans ma phototudor a écrit :J'ai l'impression que la réponse est liée à la contrainte d'avoir un carré au départ. Je suis parti du centre, avec un crayon et une feuille de papier, et j'ai reconstruit la figure de rouchka en utilisant des plis à 45°. Cela m'a donné une grille de 6x8... Est-ce que cette solution vous semble présenter de gros défauts?
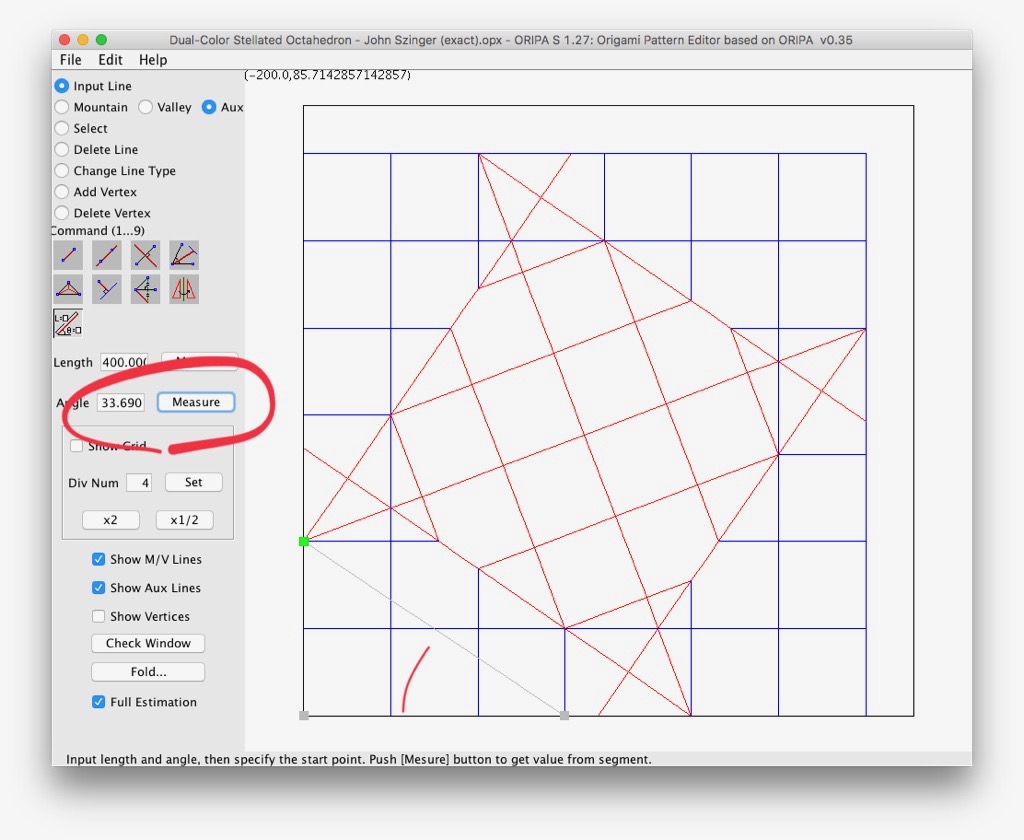
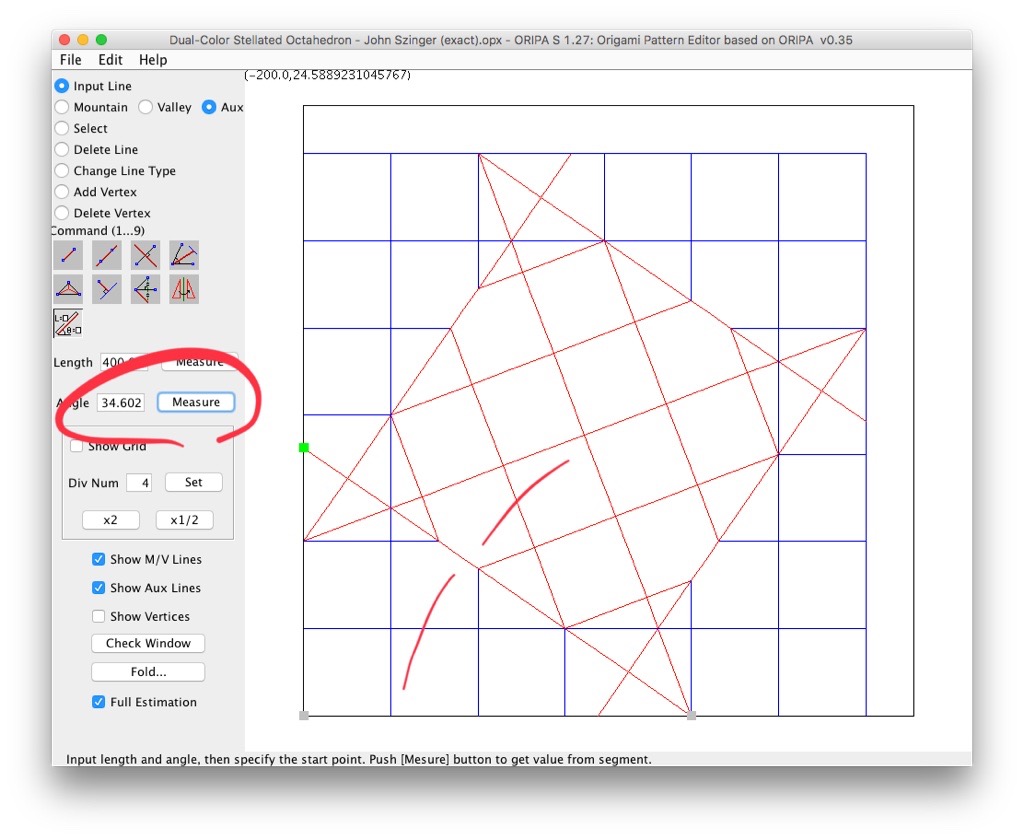
J'étais aussi en train de relire les notes de l'auteur et je crois qu'il s'emmêle un peu les pinceaux dans ses explications.rouchka a écrit :Je viens de relire ce qu'a écrit John Szinger et il parle de la pente de 3/2 (donc une tangente=3/2 ou 2/3)
or Arctg(2/3)=33.69 qui multiplié par 2 donne 67.38 ce qui est une bien meilleure approximation
Se serait il basée sur la bissectrice pour finir la construction ou est ce le résultat de la grille de 13 !?

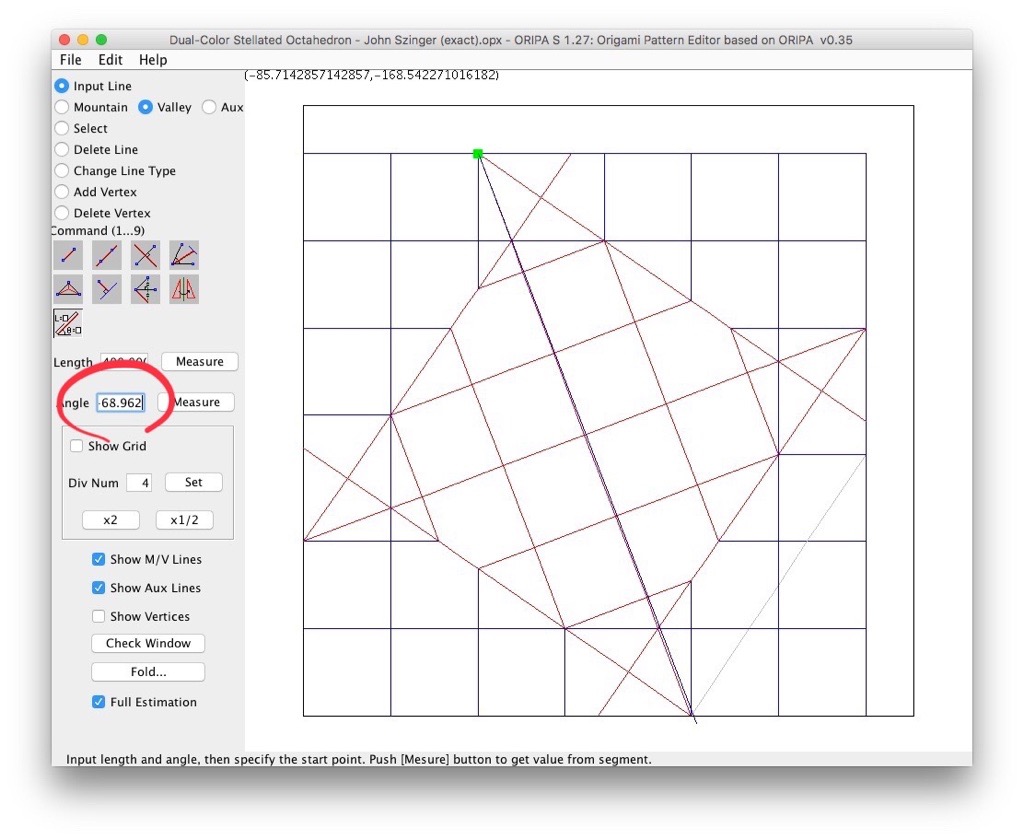
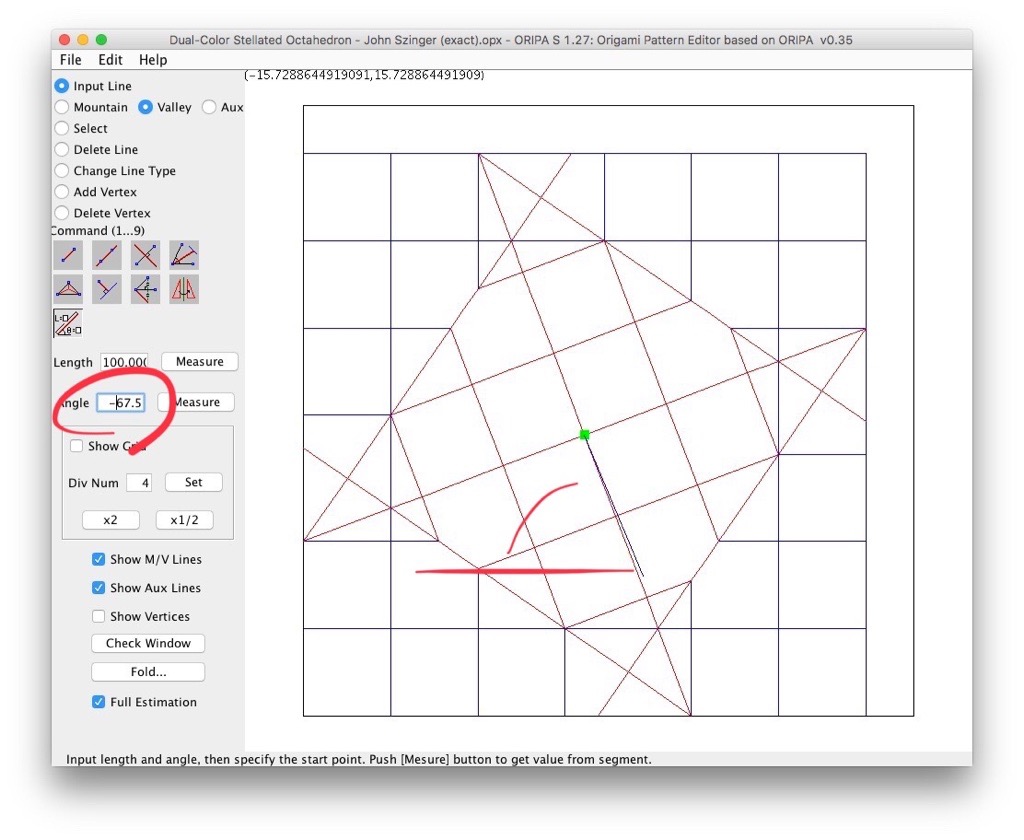
Naoki a écrit :Bon, j'ai calculé que mon fameux angle de 69.203... degrés est donné par atan(5/(2*sqrt(6)-3)). Ca me fait une belle jambe: je ne vois vraiment pas comment on pourrait construire tout ça par pliage.
Akira
Ravi que tu l'aies demandérouchka a écrit :comment as tu trouvé cette valeur?

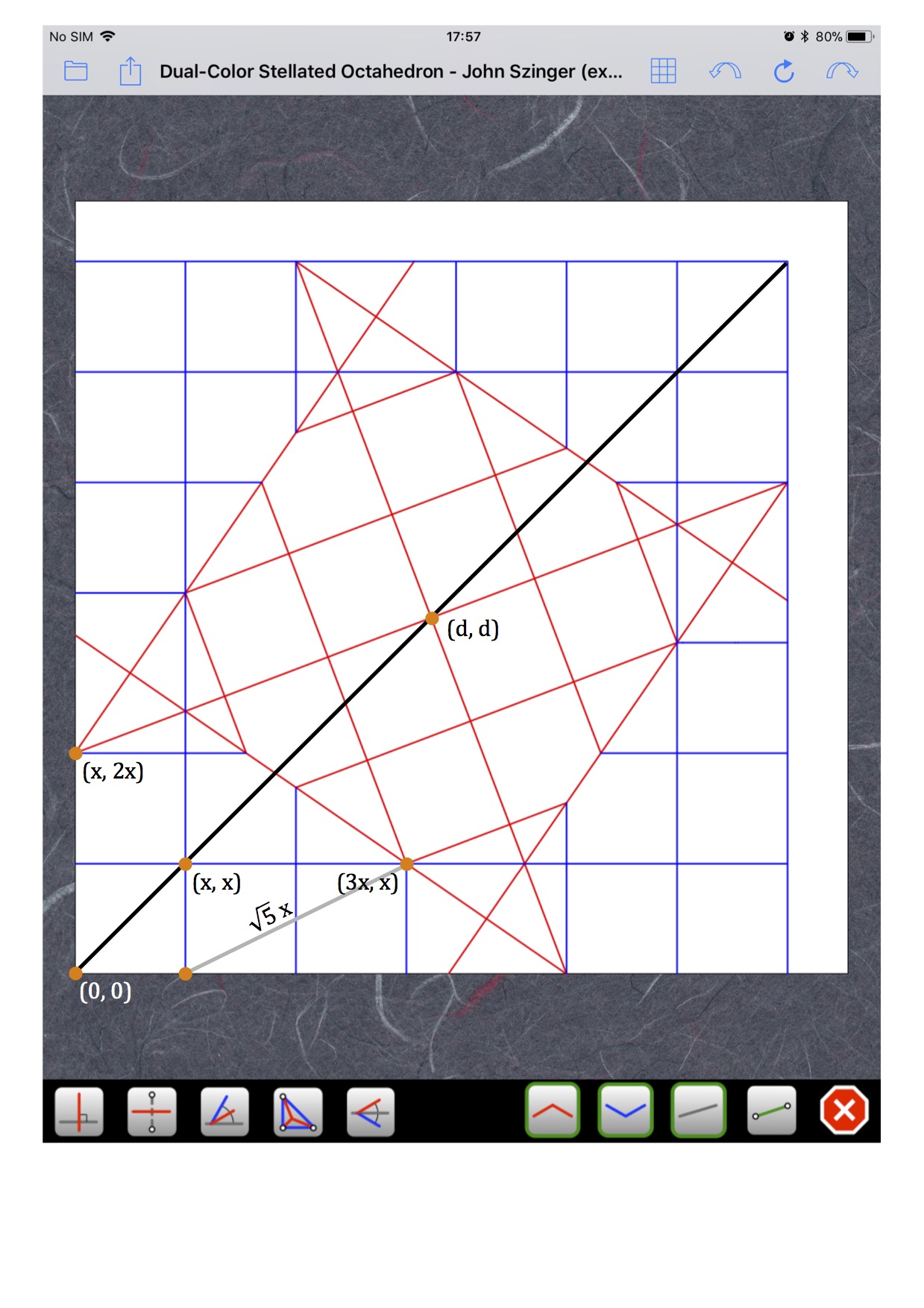
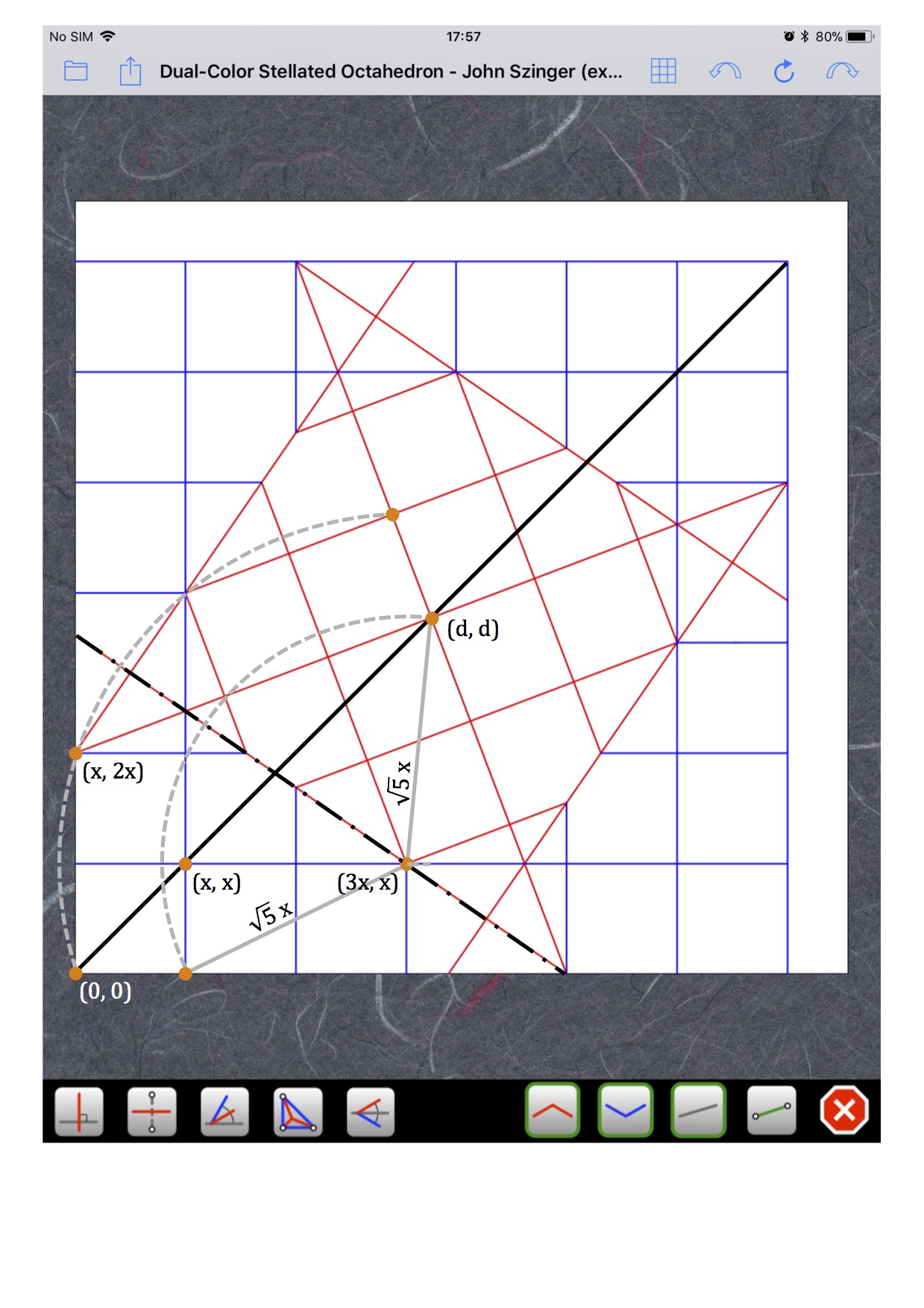
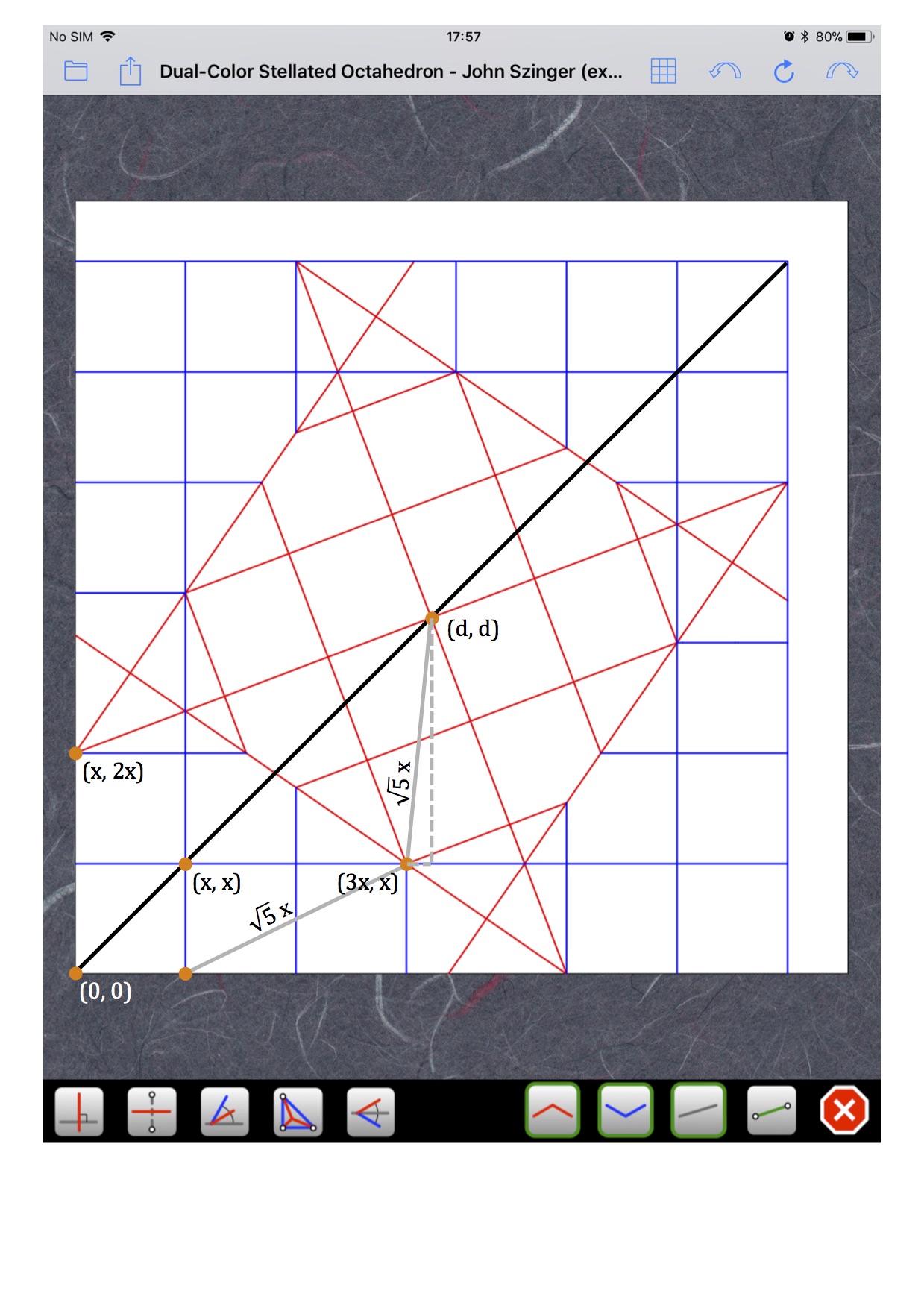
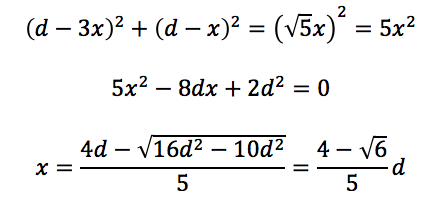
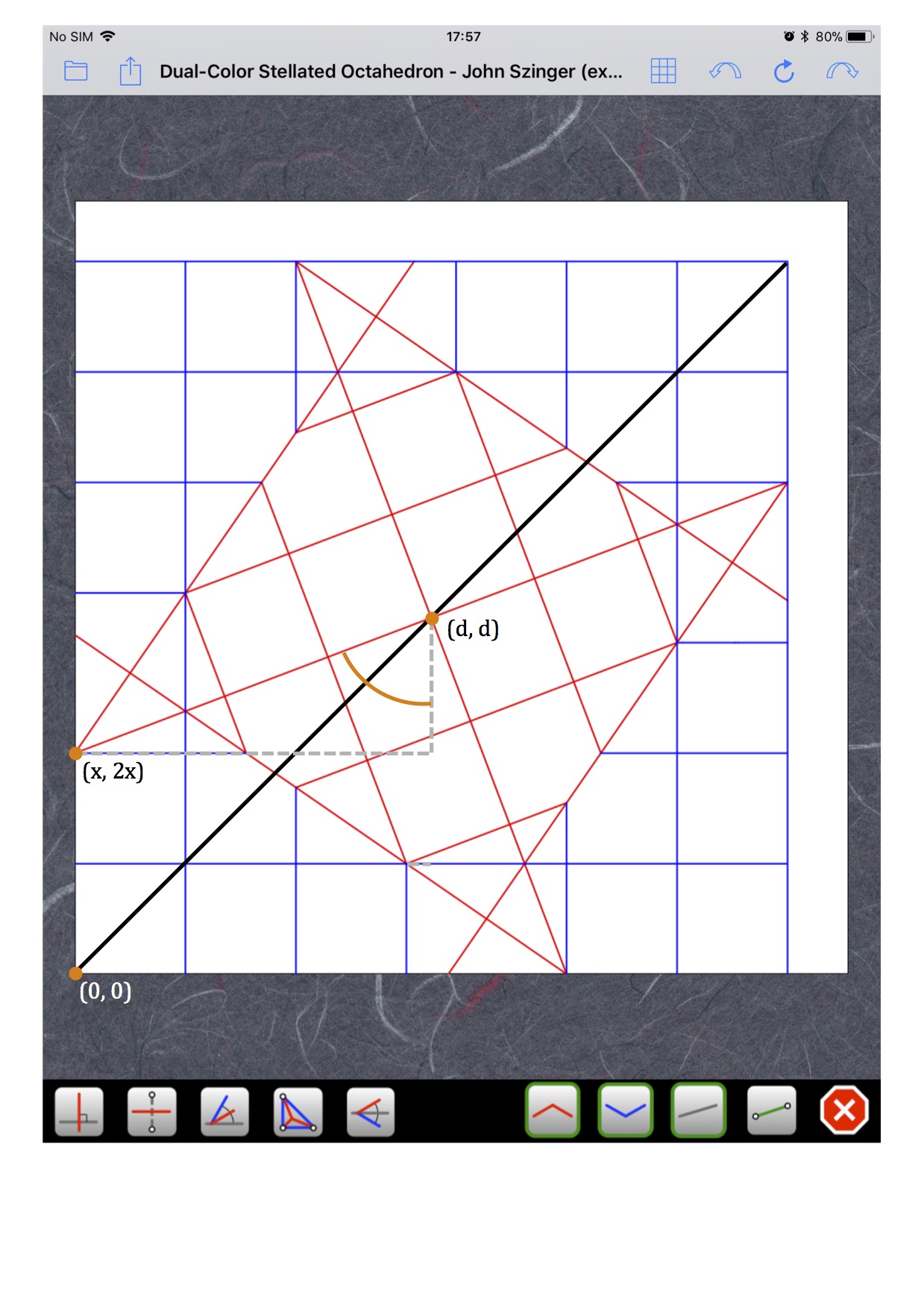
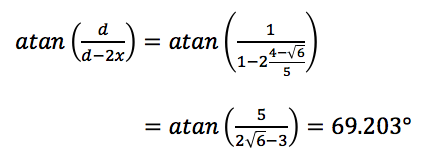
Clair et efficaceNaoki a écrit : J'espère que c'est assez clair
Akira
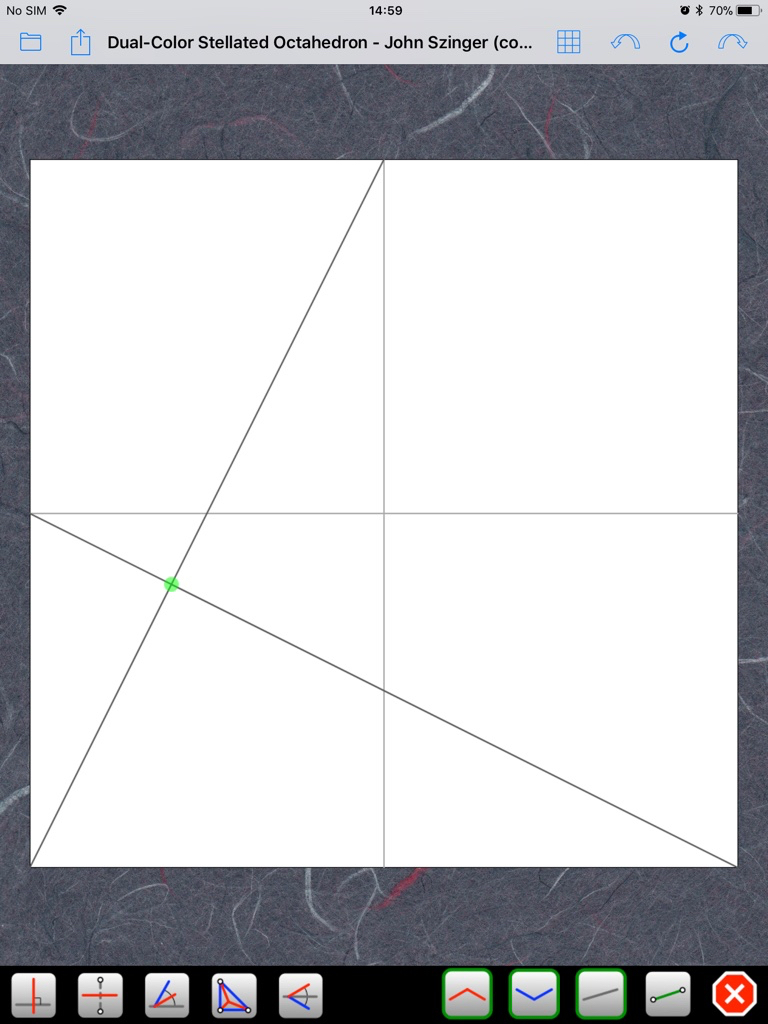





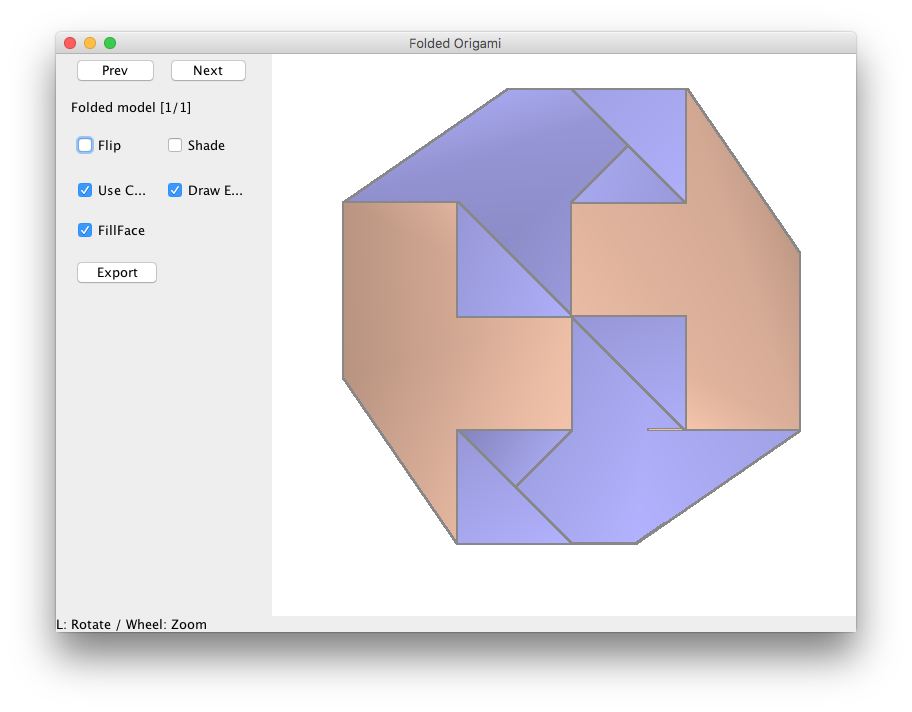
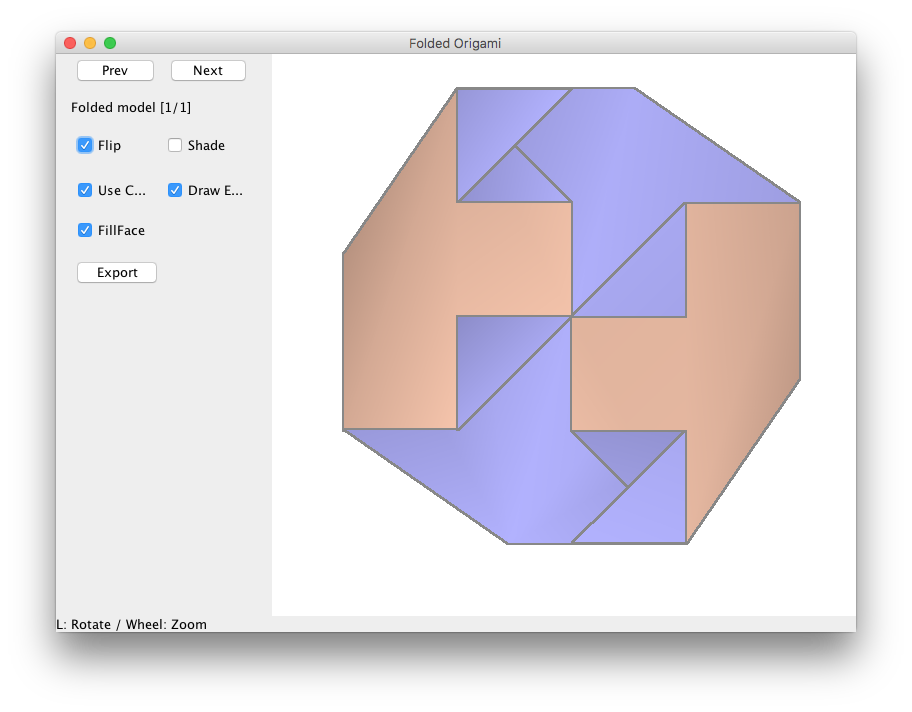
Moi c'est justement en mettant les 4 du centre en place que ça m'a aidé à amener le reste gentiment à sa place pour fermer l'ensemble sur lui meme .tudor a écrit :mais il ne faut pas commencer par les 4 du centre (ma 1e tentative). Il vaut mieux les grouper 2 par deux: un du centre et un de la périphérie.